你有没有想过,在茫茫数字的海洋中,如何找到两个向量之间的亲密程度呢?这就得靠一个神奇的工具——余弦计算器啦!今天,就让我带你一起探索这个神秘的小家伙,看看它是如何帮你解开向量之间关系的秘密的。
什么是余弦计算器?
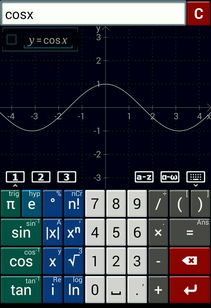
首先,得给你普及余弦计算器是一种数学工具,主要用于计算两个向量之间的夹角余弦值。这个值可以告诉我们两个向量在方向上的相似程度。简单来说,就是帮你判断两个向量是不是“好朋友”。
余弦计算器的原理
你知道吗,余弦计算器的原理其实很简单。它基于余弦定理,这个定理在高中数学里就学过。余弦定理告诉我们,在任意三角形中,任意两边长度的平方和等于第三边长度的平方加上这两边长度乘积与夹角余弦值的乘积的两倍。
在向量领域,这个定理同样适用。假设有两个向量A和B,它们的长度分别是|A|和|B|,夹角是θ,那么它们之间的余弦值就是cosθ。这个值可以通过以下公式计算得出:
cosθ = (A·B) / (|A| |B|)
其中,A·B表示向量A和B的点积,也就是它们对应分量相乘后的和。
余弦计算器的应用
余弦计算器在各个领域都有广泛的应用,比如:
推荐系统:在电商、音乐、电影等领域,推荐系统会根据用户的喜好,推荐相似的商品或内容。余弦计算器可以帮助系统找到与用户喜好最接近的商品或内容。
文本相似度分析:在搜索引擎、文本分类等领域,余弦计算器可以用来判断两篇文本的相似程度,从而提高搜索效率和准确性。
图像识别:在人脸识别、物体识别等领域,余弦计算器可以帮助计算机找到与目标图像最相似的图像。
如何使用余弦计算器?
现在,你已经知道了余弦计算器的原理和应用,那么如何使用它呢?其实很简单,只需要以下几个步骤:
1. 准备两个向量,确保它们的分量都是实数。
2. 使用余弦计算器公式计算它们的点积。
3. 计算两个向量的长度。
4. 将点积除以两个向量长度的乘积,得到余弦值。
现在,市面上有很多在线余弦计算器,你只需要输入向量的分量,就能得到它们的余弦值。
余弦计算器的局限性
虽然余弦计算器非常强大,但也有一些局限性。比如:
不考虑向量方向:余弦计算器只关注向量之间的夹角余弦值,不考虑它们的方向。这意味着,即使两个向量方向相反,它们的余弦值也可能很高。
无法处理非实数向量:余弦计算器只适用于实数向量,对于复数向量,它无法给出准确的结果。
不过,这些局限性并不会影响余弦计算器在大多数场景下的应用。
通过今天的介绍,相信你已经对余弦计算器有了更深入的了解。这个神秘的小家伙在各个领域都有着广泛的应用,帮助我们更好地理解和处理向量之间的关系。所以,下次当你遇到向量问题时,不妨试试余弦计算器,它可能会给你带来意想不到的惊喜哦!